Scientist of the Day - Alexis Claude Clairaut
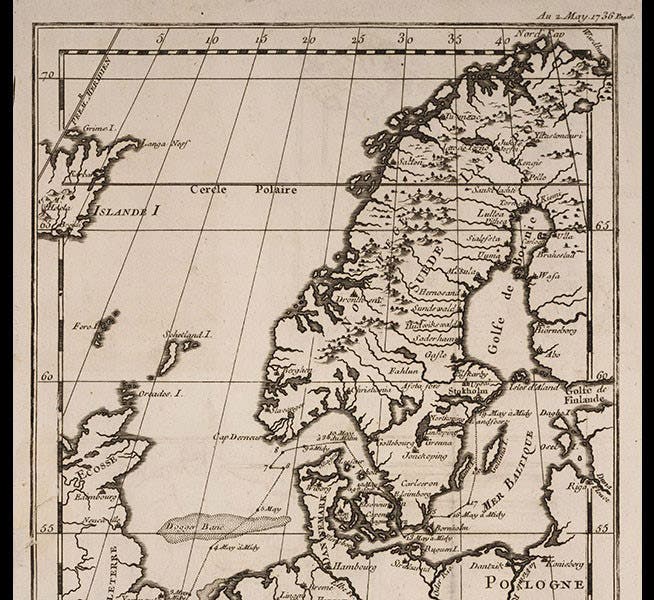
Alexis Claude Clairaut, a French mathematician, was born May 7, 1713. Clairaut was a child prodigy, giving his first paper to the French Academy of Sciences when he was just 12 years old. In 1736, he participated in the French expedition to Lapland to measure the length of a degree of latitude, for the purpose of determining whether the Earth is a perfect sphere or is flattened at the poles or the equator. The expedition was led by Pierre du Maupertuis and included Abbé Réginald Outhier and Anders Celsius, as well as Clairaut. They started at Tornea (now Tornio), at the top of the Gulf of Bothnia and measured their way north, triangle by triangle. You can see several maps of the area at our post on Outhier, who wrote a beautifully illustrated book on the expedition. We reproduce one of those maps again here, so you can get an idea of where they were working (second image, below).
Map of Scandinavia, showing the Gulf of Bothnia and the town of Tornea (Tornio), where the French expedition to Lapland was headquartered in 1736-37, from Abbé Réginald Outhier, Journal d'un voyage au nord, en 1736 & 1737, 1744 (Linda Hall Library)
The task of most of the members of the Lapland expedition was to build cairns, lay out chains, and take sightings with theodolites and zenith telescopes. Clairaut was the mathematician of the group and his job was to use the observed measurements to calculate the shape of the Earth. As it turned out, he could just as well have stayed home and made the calculations in Paris. Although he wrote and published a paper immediately upon his return in 1737 (prematurely, as it turned out), his book did not come out until 1743. It was called Théorie de la figure de la terre, tirée des principes de l'hydrostatique (1743). In the book, he showed that the observations indicated that the Earth is an oblate ellipsoid, flattened at the poles.
Title page of Alexis Clairaut, Théorie de la figure de la terre, tirée des principes de l'hydrostatique, 1743 (Linda Hall Library)
However, Maupertuis had already announced the results in his book on the expedition in 1738 (giving due credit to Clairaut and the other members of the team). What makes Clairault’s book important is that he showed there how to calculate the shape of the Earth from first principles, those principles being Newton’s law of gravitation and Huygens’ law of centrifugal force. In other words, he offered up a theorem to predict the shape of the earth, a prediction that was born out by the observations. The theorem is still known as Clairaut’s theorem and can be used to predict the shape and surface gravity of any viscous rotating mass.
Clairaut was, with Voltaire, one of the first defenders of Newtonian theory in France. He, like many others, tackled the three-body problem, trying to figure out how the Earth, Moon, and Sun interact under mutual gravitational forces. Simple-sounding, the three-body problem is notoriously difficult, but Clairaut was able to come up with a lunar theory in which a solution to the three-body problem was closely approximated. We have a second revised edition of his Théorie de la lune, déduite du seul principe de l'attraction réciproquement proportionnelle aux quarrés des distances (1752; 2nd ed., 1765), in which the title tells us that Clairaut deduced the lunar motion from the inverse-square law of universal gravitation.
Title page of Emilie du Châtelet’s translation of Isaac Newton, Principes mathématiques de la philosophie naturelle, edited for publication by Alexis Clairaut, 1759 (Linda Hall Library)
In the 1740s, Emilie du Châtelet, a brilliant woman mathematician (and mistress of Voltaire) undertook a translation of Newton's Principia into French, and Clairaut worked with her on both the physics and the math. When du Châtelet tragically died in childbirth in 1749, Clairaut saw the book through to publication, and it finally appeared in 1759 as Principes mathématiques de la philosophie naturelle (fourth image, above), a book we also have in the History of Science Collection. Surprisingly, we do not have many of Clairaut's other works, such as his two books about cometary orbits (one of them on the orbit of Halley’s comet). Given the strength of our collection in planetary dynamics, it would be nice to add to our Clairaut holdings, given the opportunity and the means to do so.
Dr. William B. Ashworth, Jr., Consultant for the History of Science, Linda Hall Library and Associate Professor emeritus, Department of History, University of Missouri-Kansas City. Comments or corrections are welcome; please direct to ashworthw@umkc.edu.
